トランジスタのショットノイズモデルの詳細と限界 &

■参考
トランジスタのショットノイズの効果 - SonofSamlawのブログ
1.トランジスタ(BJT)のバイアス回路とベース電流
トランジスタの入力部のノイズが、どうして図0の(a)のようにされるのか?
さらには、入力に全く関係のないコレクタ電流のショットノイズも繰りこんだ(b)が出てくる。そもそも、このモデル自体が数学的な強引なモデルにすぎないということなのだ。つまりこう書いておき、つじつまを合わせる、ということなのである。簡単に言えば、2つの自由度をノイズ電圧と電流に、単に分担させ、つじつまを合わせているだけとも言える。このこと、図0(b)の詳細は、
トランジスタ、OPAMP、オペアンプ回路のノイズ解析 - SonofSamlawのブログ
をご覧ください。
本ブログでは、図0(a)のInb、つまり、ベース電流のショットノイズのモデル化の正当性と影響について考えることにする。
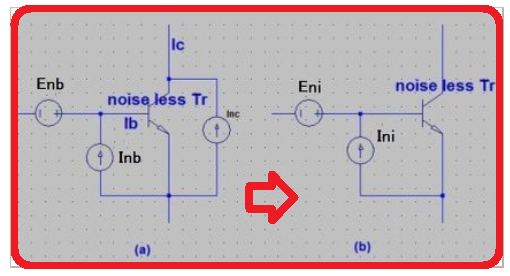
図0 トランジスタのノイズモデル
まず図1をかんがえる。
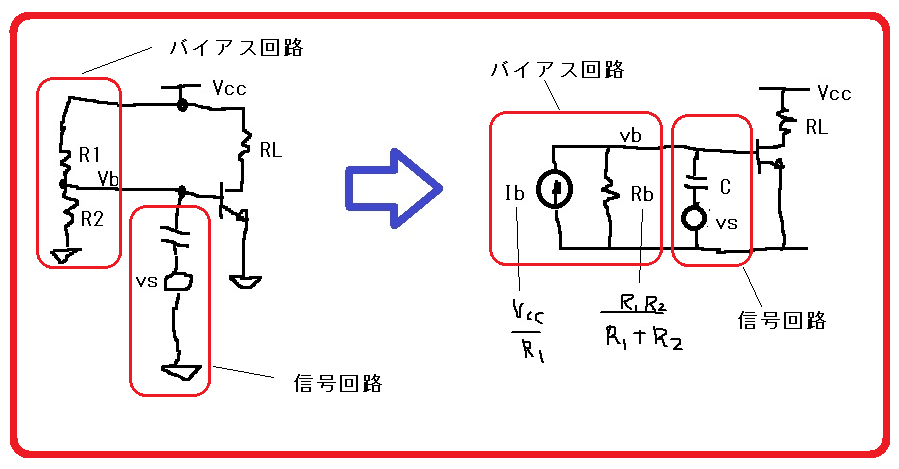
図1 バイアス、信号回路の等価回路
テブナンの定理から、バイアス回路は図2になる。
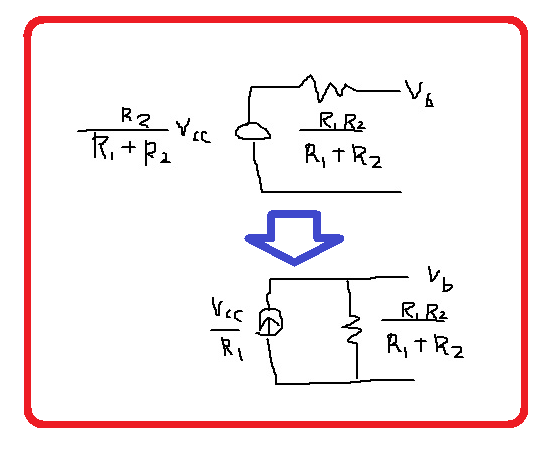
図2 テブナンの等価回路の2形態
2.ベース電流によるショットノイズのモデル化
ベース電流のショットノイズは、図3のようにモデル化できる。
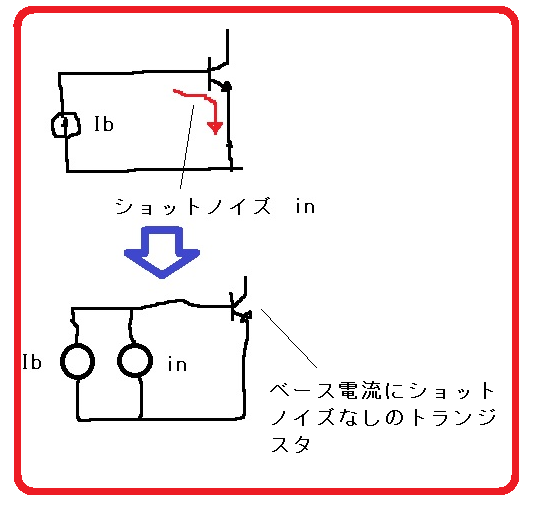
図3 ベースのショットノイズのモデル
ベースのショットノイズの実効値電流周波数密度は、バイアス電流のルートに比例する。
in(実効値の周波数密度))=√(2qIb) (A/√Hz)
q:電子の電荷
このことから、図3のように考えることによって、あらゆる構成でも満たされるかどうかがわからない。バイアス電流とは別に考えなければいけない。
また、ベースーエミッタ間電圧のDC値Vbeを一定にした場合も問題ない!この場合もベース電流にはショットノイズが生じるが、Vbeが変化ないためコレクタ電流にはノイズは現れない。
この場合、
ic=β*ib(ショットノイズ)
ではなく、
ic=gm*vbe
としなければいけない。
しかし、図3のモデルでは、
ic(ショットノイズ)=β*ib(ショットノイズ)
が成り立つ。難しいところだ。
ベース広がり抵抗によるジョンソンノイズも考慮すると図4になる。
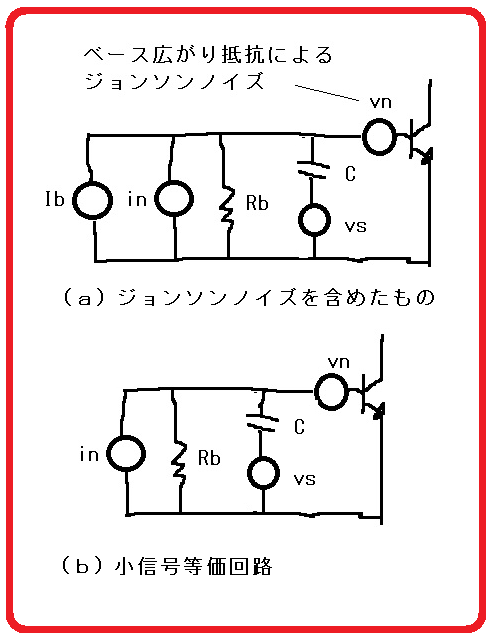
図4 すべてを考慮した等価回路
このモデルで、Cのため高い周波数でショットノイズは無くなる。実際はどうなのか?ベースーエミッタ電圧vbeがコンデンサでショートされるんでそうなるかもしれない。
上のショットノイズのモデルにおいて、実際の接合部分の動作から考えて、この外部電流源モデルには矛盾はないのだろうか?
ショットノイズが発生しているということは、それが接合部の事情であるにしても、それに相当するvbeも変化しているということだ。ベース電流とvbeには関係がある。ベース電流はvbeがあるから流れるのだ。ベース-エミッタ間につけられた容量Cも動作するので、vbe変化も緩和(打ち消され)され、ショットノイズも緩和される、フィルタされるとおもわれる。ショット効果の負帰還で、端子電荷・電圧が、その変化を打ち消すような電荷が供給されるということだーー>上の等価回路は正しいと思える。
しかし、この外部電流ノイズモデルでは、実際のvbeとベース電流の関係が逆転している感じがする。
外部電流モデルーー>vbeが大きいとき、ベース電流大きい。
実際 ーー>ベース電流が流れない(せき止められる)とき、
電流源からの電荷がベースに溜まるんで、vbeが大きくなる。
実際の場合、ショットノイズは、接合部で「電流がせき止められる」ことで発生しているので、こうなると思う。接合に電流がないときには、ベースに電荷がたまり、vbeが大きくなる。つまり、上の等価回路と逆になってしまう。ランダムノイズなんで無視してもいいのかもしれない。実効値のみが問題である白色ノイズでは問題にしないでいいのかもしれない。
図0(a)のinb、図4のinは信号vsによっても変わることを注意しなければいけない。ショットノイズは電流に比例するからである。
inはどこに入れてもよいが、vnはそうではない!
図0(a)のコレクタのショットノイズincも、コレクタ電流のショットノイズが、コレクタ電流源に並列につながれたノイズ電流源でモデル化できることを示している。このノイズ電流incも、コレクタ電流で変化する。
3.ショットノイズメカニズムの再度検討
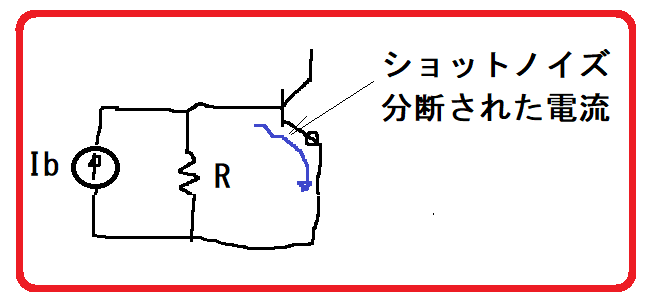
図5
図5で考えると、原理的で定性的なメカニズムでは、be間で電流が分断されることによるショットノイズinは、ベースーエミッタ間電圧vbeを変化させる。このとき、ベースーエミッタ間がショートされていればvbeが変化せず、つまり電荷はそちらへ逃げ、打ち消されてノイズ電流は緩和される、もしくはなくなる。Rが有限の場合でもRの大きさによりノイズ電流は緩和される。
図5の場合、Rが大きいとこの効果は少なくなる。
さらに考えてみると、
別なメカニズムとして、ショットノイズ電流が、上記のようなメカニズムでvbeを変化させ、それがコレクタ電流ノイズをうみだしている、というものである。つまり、コレクタショット電流icnは、
icn=gm*vben
vben=in*Rin=in*β/gm
となる電圧を生み出している。
この方が正しいのかもしれない。
ベースバイアス電流がショットノイズの原因である。構造上バイアス電流が流れれば発生してしまう。広い通りから、pn接合部では人一人しか通れない道になるのだから。
このベースショットノイズ電流は、直接にはコレクタ電流に影響しない。しかしこのためにvbeが変化すると思われる。ショックレイの理論では、コレクタ電流はvbeのみで生じるからだ。このvbe変化がコレクタノイズ電流icnの原因になると考える。
ベースーエミッタ間にショットノイズ電流inが流れれば、ショックレイ理論では、そのときvbeがあると考えられる。
vben=Rin*in
Rin=β/gm
こう考えてみる。
inにより、ベースエミッタ間ノイズ電圧vbenが生じる。一般に、
ic=gm*vbe
という関係があるから、
これによるコレクタ電流ノイズicnは、
icn=vben*gm
となる、これがベースショットノイズ電流inに起因するコレクタノイズ電流icnである。ここで、
vebn=in*Rin=in*β/gm
であるならば、
icn=vben*gm=in*β
となる。
*ベースショットノイズ電流があっても、vbeが変化しなければ、たとえばコンデンサでb-e間をショートしてしまえば、その帯域ではコレクタ電流に影響はしない、ということだ。
まとめると、図5-2になる。

図5-2 モデルの正当性
・・・どうだろうか?
バイポーラトランジスター(BJT)の原理(メカニズム) - SonofSamlawのブログ
によれば、図6のようになり、ベースショットノイズがコレクタ電流に直接影響がないことがわかる。しかし、ベースショットノイズによるvbeが生じ、これがコレクタ電流のノイズになるという推論である。
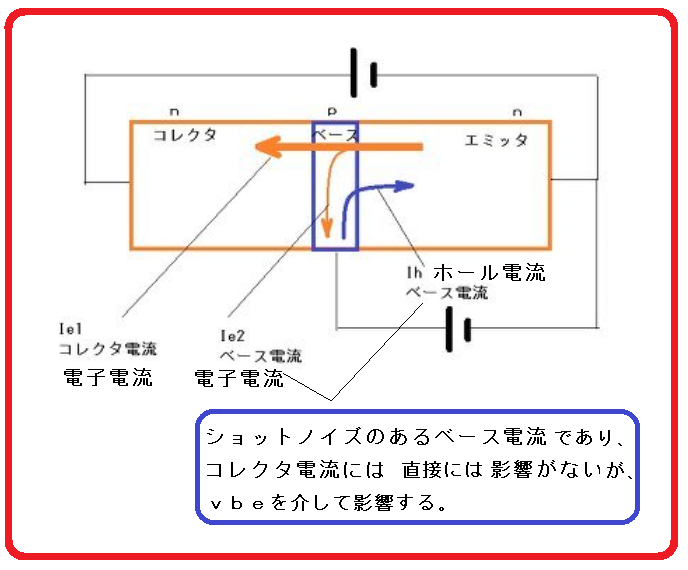
図6 トランジスタの構造
こんなメカニズムである。

図7のモデルはこれをうまく表現できている。inはバイアス電流がすべてベースに流れた時のショットノイズ電流である。R=∞で、
ベースショットノイズ=in
となる。このモデルでは、ベースに流れた電流のβ倍がコレクタノイズ電流になっていると考える。
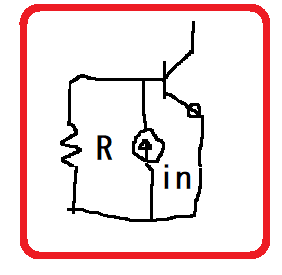
図7
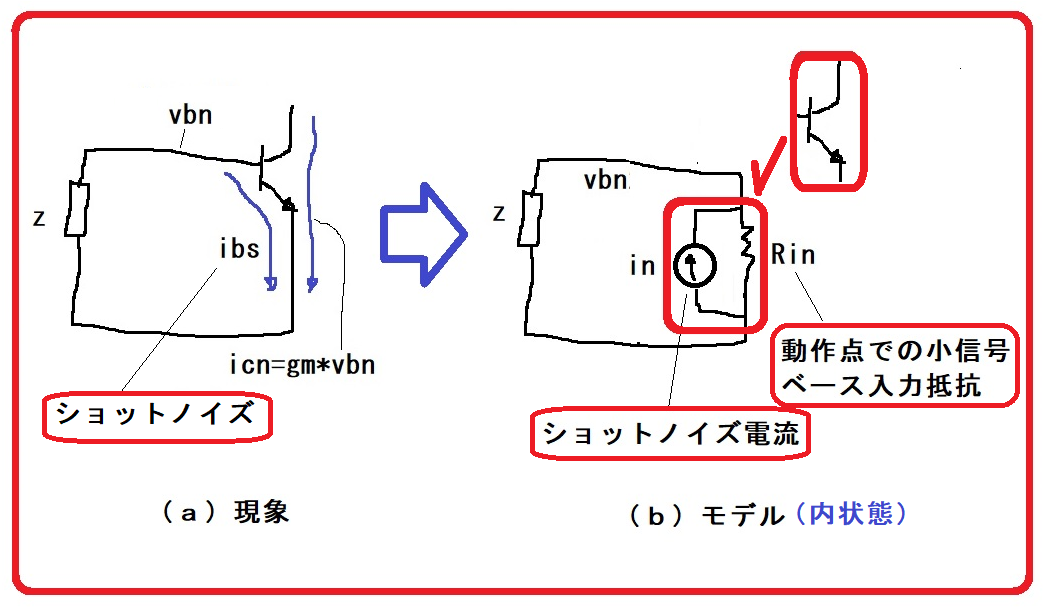
図7-2(世界的なモデル)
ショットノイズについての1957年の論文 - SonofSamlawのブログ
によれば、とても難しい議論が始まってしまう。物理屋による熱力学からの考察・理論からのモデルである、半導体ダイオードのショットノイズモデルは、図7-4になる。ここで、正弦波以外の信号に、スタインメッツの交流理論が安易に使われていることが疑問でもある。
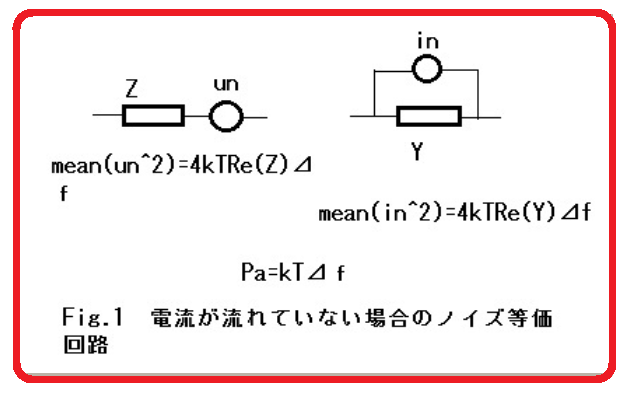
図7-3
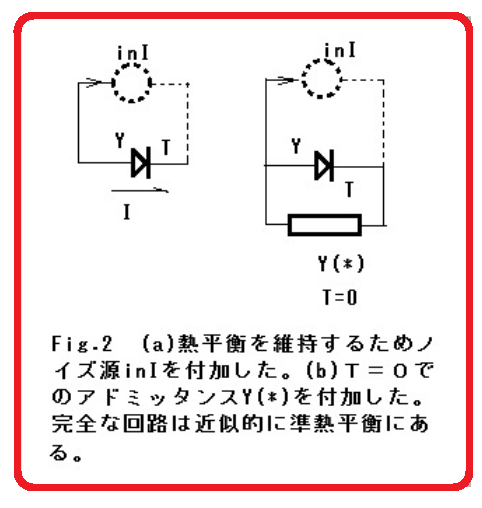
図7-4
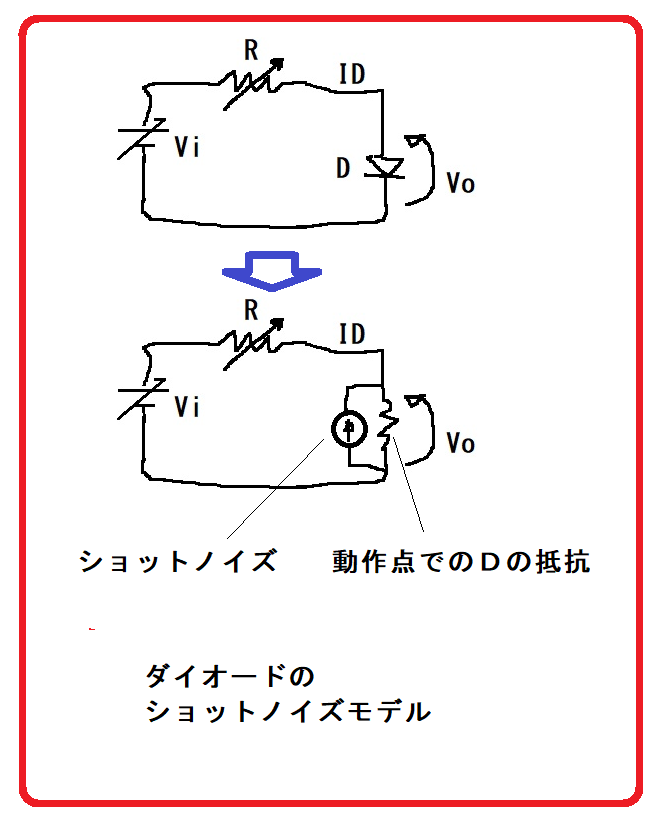
図7-5 世界的なダイオードのショットノイズモデル
図7ー2,3の等価回路は過渡現象を近似して得られた等価回路である。実は瞬間的起こっていることではなので、順番に起こっている。
4.エミッタでバイアスする場合
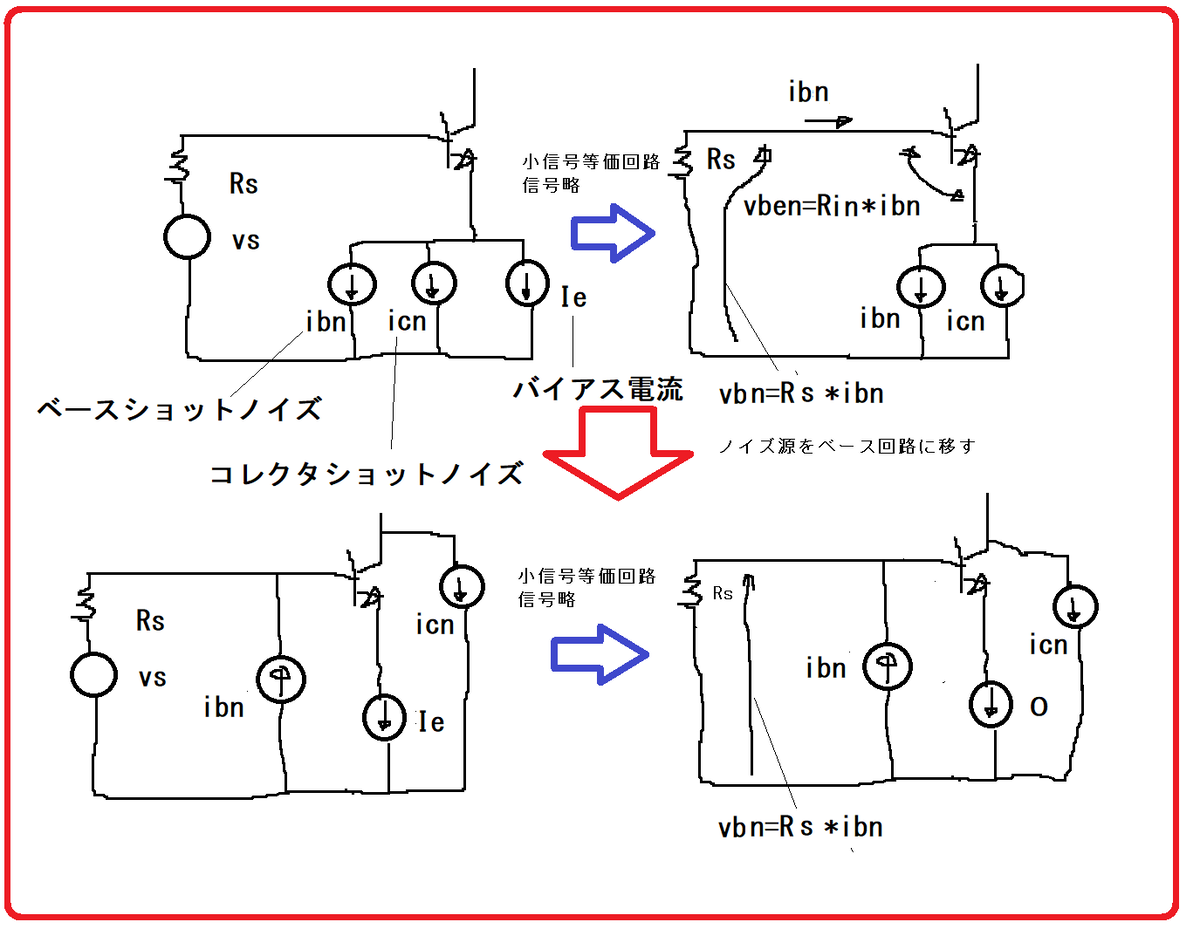
図8
これは全く正しくない。入力側の条件に依存していない。入力がショートされてもベースにはibnが流れてしまう。
5.差動回路の場合
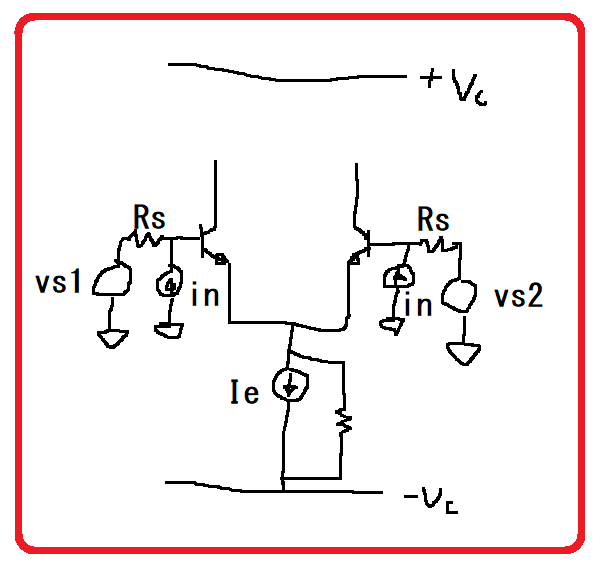
図9
図10ではB-E間にショットノイズがあってもコレクタ電流には影響しない。この等価回路では、それが正しく表現されている。
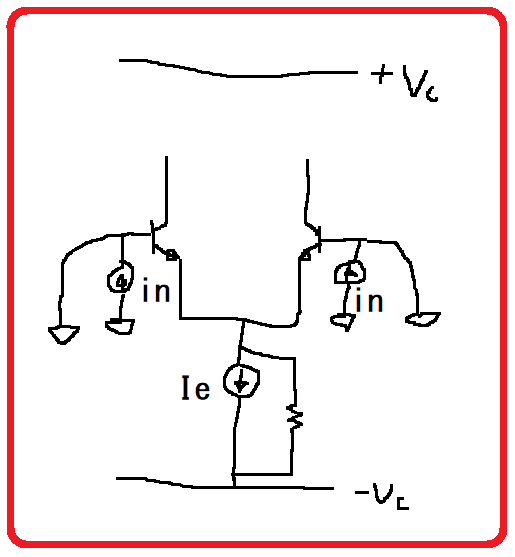
図10
■参考に
トランジスタ回路のノイズ解析
トランジスタ回路のノイズ解析 - SonofSamlawのブログ (hatenablog.com)
FETの等価INノイズ電流は、なぜ高域で上がるのか?
FETの等価INノイズ電流は、なぜ高域で上がるのか? - SonofSamlawのブログ
FET入力オペアンプの電流ノイズの測定
FET入力オペアンプの電流ノイズの測定 - SonofSamlawのブログ (hatenablog.com)