
FETアンプの等価IN電流ノイズが周波数で上がっていきます!
どうしてでしょうか?
解明しました!
参考
トランジスタ回路のノイズ解析
トランジスタ回路のノイズ解析 - SonofSamlawのブログ (hatenablog.com)
FET入力オペアンプの電流ノイズの測定
FET入力オペアンプの電流ノイズの測定 - SonofSamlawのブログ (hatenablog.com)

この本によれば、

■参考
トランジスタのノイズモデル
トランジスタのノイズモデル - SonofSamlawのブログ
図6の(a)において、Enbはベース広がり抵抗rbbによるノイズ電圧の実効値、Inbはベース電流Ibによるショットノイズ電流の実効値、Incはコレクタ電流Icによるショットノイズの実効値である。
(b)においてはそれらをすべてトランジスタの外につけた電圧源と電流源のみで表現している。(b)の2つのノイズ源は次のように定義することにする。
Eni^2 = Enb^2 + Inc^2/gm^2 (J-1)
Ini^2 = Inb^2 + Inc^2/β^2 (J-2)
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
ここまでが引用です。あとは私の意見です。
ここで肝心なことは、Incは、Inc/gmというノイズ電圧源とInc/βというノイズ電流源という外部ノイズ源に移されるということである。IN端子に抵抗Rsがつながれたとき、その抵抗の大きさに応じて2つは影響を分担する。Rs≒0のときInc/gm、Rsー>∞のときInc/βが支配的になる。しかし、Inc自体はRsには関係なく存在する。このことを矛盾なく表現しなくてはいけない。下に示すようにそれは証明される。En b,IInbについても同じである。Rs≒0のときにはEnbが、Rs->∞のときInbが支配的になる。
このことを図7に示し、そこから証明してみよう。

図7 Rsを考慮した場合
ここで、Incの和はこの2つが当然ながら、相関があるので、2乗和は通常のの和の2乗になることに注意すると、、図7-(b)では、(j-1,2)式から、

つまり、図7-(b)と(j-1,2)式から計算したIcは、図7-(a)から計算したものと一致している。

図9 BJT IN換算ノイズ電圧Eniの測定
図9の回路でまずIN換算電圧ノイズEniを測定する。図9でVoを測定する。回路ゲインGは測定されるのでgm*RLはそのときわかる。
Eni=Vo/(gm*RL)
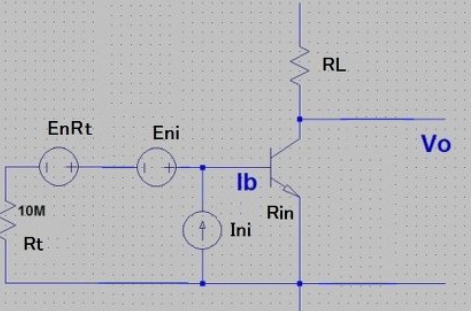
図10 BJT IN換算ノイズ電流Iniの測定
図10の回路でIN換算電流ノイズIniを測定する。Rtのノイズ電圧EnRtとEniは既知とする。このとき、EniとIniの中には相関あるノイズが含まれているが無視することにする。このとき、実際の値は最大でこの2倍になる。通常はそれ以下になる。
(Vo/(gm*RL))^2
=(Ini*Rt*Rin/(Rt+Rin))^2
+(EnRt*Rin/(Rt+Rin))^2
+(Eni*Rin/(Rt+Rin)^2
から、
( Ini*Rt*Rin/(Rt+Rin))^2
=(Vo/(gm*RL))^2
ー(EnRt*Rin/(Rt+Rin))^2
-(Eni*Rin/(Rt+Rin)^2
Ini =√((Vo(Rt+Rin)/(gm*RL*Rt*Rin))^2
ー(EnRt/Rt)^2-(Eni/Rt)^2)
=√((Vo/(gm*RL*(Rt//Rin)))^2
ー(EnRt/Rt)^2-(Eni/Rt)^2)
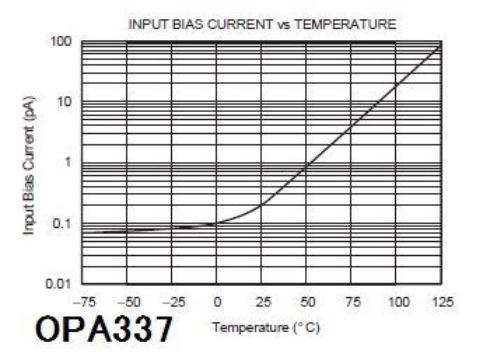
上の参考図3、jFETIN型OP AMPのIniの周波数特性が3kHzあたりからあがっているのはこのためなのかもしれない。jFETのゲートとソースは高い抵抗と容量の直列だろうから、これによるゲート電流とドレイン電流でβが定義できる。このβはBJTと違い数kHzから下がる。というより、それ以前ではBJTと比べ物ぬならないほど大きい。そこから、ゲート容量のために急激に(20dB/decで)下がっていく。
このため、BJTと違い Inc/β は、高域で上がっていくのだろう。
しかし、一般にはゲートインピーダンスの実部のせいだとされているのだが・・・
こうして測定されたIniは実際の電流ノイズ、つまりInbとは違ってくる。しかし、測定できるにはこのIniしかない。上の参考図3における電流ノイズもIniであると思われる。もしInbを測ろうとするならば、図10のRtの電圧を別のAMPで測らなければならないが、そのAMPのノイズが入ってきてしまう。このあたりのこともこの問題をいっそうむずかしくしている。
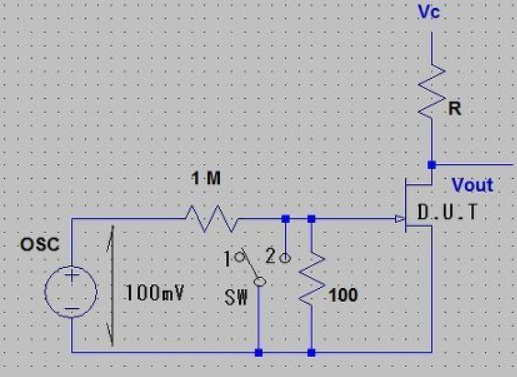
図11 ノイズ電圧測定

図12 ノイズ電流測定

図13 OPAMPノイズ電流の測定回路

k=1.38E-23
でかんがえると、T=300,R=20kとして
√(4kTR)=18nV
■OPAMPで考える

内部ノイズEn2は単に1/AvにしてEn1に加えるだけではなく、等価電流ノイズとしても加えるようにしなくてはならない。
力端子のノイズ電圧:En1
入力端子のノイズ電流:In1
内部ノイズ源によるOUT電圧:En2
これは、En1とIn1とは無関係である。
等価入力ノイズ電圧:Eni
等価入力ノイズ電流:Ini
とし、
Eni^2 = En1^2 +En2^2/Av^2 (J-3)
Ini^2 = In1^2 + En2^2/(Rin*Av)^2(J-4)
と定義すると、
eon^2
=Av^2*En1^2*(Rin/(Rs+Rin))^2
+Av^2*In1^2 *(RsRin/(Rs+Rin))^2
+ (Av*(En2/Av)(Rin/(Rs+Rin))+ Av*En2/(Rin*Av))(RsRin/(Rs+Rin)))^2
=Av^2*En1^2*(Rin/(Rs+Rin))^2
+Av^2*In1^2 *(RsRin/(Rs+Rin))^2
+ (En2*Rin/(Rs+Rin)+ En2*Rs/(Rs+Rin))^2
=Av^2*En1^2*(Rin/(Rs+Rin))^2
+Av^2*In1^2 *(RsRin/(Rs+Rin))^2
+ En2^2
となり、矛盾はないことがわかる。