
ライター:mpcsp079さん(最終更新日時:2016/4/17)投稿日:2015/3/5
平成19年度電験三種「機械」の回答
Pによる等価電荷密度
B問題
●問-15
6極、定格周波数60[Hz]、電機子巻線がY結線の円筒形同期電動機がある。この電動機の一相当たりの同期リアクタンスは3.52[Ω]であり、また、電機子抵抗は無視できるものとする。端子電圧(線間)440[V]、定格周波数の電源に接続し、励磁電流を一定に保ってこの電動機を運転したとき、次の(a)及び(b)に答えよ。
(a) この電動機の同期速度を角周波数[rad/s]で表した値として、最も近いのは次のうちどれか。
① 12.6 ② 48 ③ 63 ④ 126 ⑤
253
(b) 無負荷誘導起電力(線間)が400[V]、負荷角60[°]のとき、この電動機のトルク[Nm]の値として、最も近いものはどれか。
① 115 ② 199 ③ 345 ④ 597 ⑤ 1 034
http://avalonbreeze.web.fc2.com/35_03_02_synchronous_motor.html
より、下図を引用する。
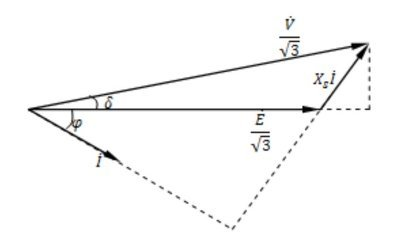
機械出力Pmは、E,Vを線間電圧とし、
Pm/3=(E/√3)*I*cosΦ
cosΦ=(V/√3)sinδ/(Xs*I)
だから、
Pm/3=(E/√3)*I*(V/√3)sinδ/(Xs*I)
=(E/√3)*(V/√3)sinδ/Xs
Pm=E*Vsinδ/Xs
■解
(a)
Ω=2πN/60=2πf/(p/2)
=2π*60/3=126rad/s
(b)
T=Pm/Ω=E*Vsinδ/Xs/Ω=344