
ライター:mpcsp079さん(最終更新日時:2016/3/29)投稿日:2012/11/30
.
コンデンサ問題 充電されたコンデンサに並列にコンデンサをつけると?
■ 電荷の溜まったコンデンサに並列にコンデンサをつけるとどうなるか??? という問題を考えてみます。
この問題はどんな本にも書いていないし、誰にきいてもわかりません。
http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1297861502
参照
> 充電されたコンデンサーと充電していないコンデンサーをつなぐと
> 電子が移動して、2つのコンデンサーは同じ電位差になりますが、
> 充電されていたコンデンサーは異なる電荷をもつ極版どうし引力で
> 引き合っているのに、どうして充電されていないコンデンサーへ引力
> を 無視して?電子が移動することができるのですか?電流は電位
> の高いところ から低い所には流れますが電位差の大きいところから
> 小さいところには 流れないと思うんですが
いい質問です。
■ それでは考えていきましょう。ゆっくりいきますのでよろしく・・・

図1 各径路での積分(電圧)
図1は電荷Qのたまったコンデンサです。宙に浮いています。コンデンサの部品は導体です。つまり、少しでも電位差があれば、つまり、電界があれば電子が動き、それを中和してしまいます。
点電荷の作る電界を周回積分しても0です、それらの合成電界についても同じです、
各極板内は同電位です。もしそうでなければさっそく電子がそれにそって移動し打ち消してしまうからです。
以上のことから、2つの極板間のどのような経路に沿っての
∫E・dl
は、すべて同じになると言えます。たとえば径路aとbなど。その共通の値が、極板間の電位差、電圧というものです。

それでは、こんどは、極板間に図2のように電圧Vを加えてみましょう。
図2のごとく、電極や導線には、電荷が分布します。前述のように、極板や導線はつながっていれば同電位です。ですから、2つの極板間でのあらゆる径路での
∫E・di
の値は同じで、それはVとなるはずです。それは加えたVの定義からもあきらかです。
このような考察から、極板の間隔の大きいところでは、電荷は小さいと言えます。つまり、容量の小さいコンデンサに蓄えられる電荷は小さい、ということなのです。
それでは、上の疑問、
> 充電されていたコンデンサーは異なる電荷をもつ極版どうし引
> 力で 引き合っているのに、どうして充電されていないコンデン
> サーへ引力 を 無視して?電子が移動することができるので
> すか?
にこたえるとしましょう。

図3 充電されたコンデンサ
図3が充電されたコンデンサです。

図4 容量が小さいコンデンサをつなげてみる
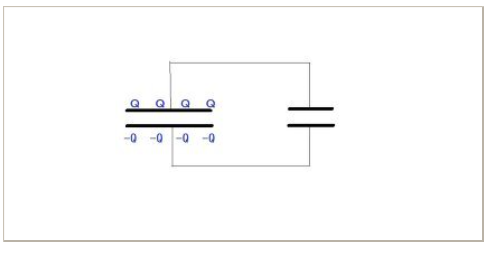
図5 つなぐ、電荷移動前

図6 つなぐ
図5のように、2つのコンデンサが導線でつながれると、図2と同じになり、両極板のどの場所も同電位となり、両極板間のどのような経路での電位差もすべて等しくならなければなりません。つまり、両極板の各点には、それを満足させるような電荷が振り分けられなければなりません。
そこで疑問、
> 充電されていたコンデンサーは異なる電荷をもつ極版どうし引
> 力で 引き合っているのに、どうして充電されていないコンデン
> サーへ引力 を 無視して?電子が移動することができるので
> すか?
です。左のコンデンサの電荷は+-で引き合っています。しかし+-の電荷がいるのです。これは+-の電荷が引き合うことによっている、というより、+-の電荷が引き離されて存在している、とも言えるのです。これは電圧を生みます。この+-の電荷と導体でつながっている部分の間には同じ電位差、電圧が生じます。すると、そこには電荷が生じなければなりません。それは、初めにたまっていた電荷からもってこられます。
もし、このコンデンサから図5のように、導線を引き出してやれば、その導線間にも電位差が生じなくてはならないのだから、電荷が「配分」されなければなりません。

図7 aにだけ電荷があった場合
ここで、図7のようにaにだけ電荷があった場合を考えましょう。そして、図のような積分路を考えましょう。E・dlをこの積分路で積分しますと、それは=0でなければなりません。導体内はE=0ですから、aとcの積分路だけです。この2つの積分結果は、値が同じで、符号が逆でなければなりません。つまり、C2にも電荷が配分されるのです。その分C1の電荷は少なくまります。
■
まだわかりにくいですね。上と下の導体は電位差があります。C2の側もそうです。ですから、C2にも電位差に応じた電荷がたまります。それはC1から配分されます。C1,C2の電位差が等しくなるように配分されます。
■
まだわかりにくい? 図7のb、dは金属ですからその中で電界は0ですね。もし、電界があればすぐさま電子が動いてそれを打ち消してしまう。初めにaだけに電荷が集まっていたとします。そして、cには集まっていなかったとします。すると、b、c、dの径路はすべて電界なしですね。すると、aだけが段差があり、その他では段差なし、という矛盾が出てきます。つまり、cにも電荷が集まる必要があります。それはaにいる電荷が配分されるしかありません。そして、aの電位差=cの電位差 という状態になるまで移動します。
■
2つの導体の間にはどこでも電界があります。aとcだけに電界があるわけではない。この電界を2つの導体の間で積分すれば、必ずどこでも同じ値になります。これが2つの導体の間の電位差なのです。 これは点電荷の重ねあわせである、と考えればわかります。
導体の中は等電位であるのは、電界がないから。もし、電界があったなら、自由電子がそれを打ち消すように動くからです。
C2をついで、平衡状態にたったときには、C2の極板間にもC1と同じ電圧がかかります。導線内は同電位だからです。すると
Q2=V2/C2
という電荷が必要になります。これはC1の電荷がもってこられます。もっと正確に言えば、C1とC2をつなぐ2本の導線の間にも電荷が充電されています。これは考えないとすれば、最終的に、
Q1+Q2=Q(初めC1に充電されていた電荷)
Q1=C1*V1
Q2=C2*V2
V1=V2
が満足されなくてはいけません。
ここで鍵となる考えは、
①2つの+-の電荷がたまった金属の間の電位差はどこの間でも同じである。
②導線内の電界は=0である。そうでなければそれをうちけすように電子がうごくから。
③電位差の原因は+-の電荷であるから、たとえば導線の途中にCがつながっていれば、
Q=C*V
の電荷が充電されるひつようがある。
④これらの電荷は、すべて初めに充電されていたC1の電荷から、配分される。
■
図7の状態でc部をショートしたらどうでしょうか? a部の電荷+-Qは互いに引き合っているのでそのままでしょうか?
もう一度考えましょう。図7では、上の導体と下の導体にそれぞれ+QとーQがいるのです。しかし、c 部分の間隔が離れている場合、a部分に特に電荷が集まっていたのです。それは間隔が小さいためです。
間隔が小さいと(たとえばaのように)、対向導体の電荷とより引き合います。だからたくさん集まります。さらにcのような部分ができると、そちらでも引力が強くなるので、電荷が集まります。これを難しく言えば、aの電圧とcの電圧が同じになったところで平衡します。
もし 、cをショートすると、すべての電荷が移動してしまいます。aで引き合っていても、ショートされたcの方が間隔が狭い(=0)ので勝ちます。 そして、完全に移動して、中和してしまいます。