コルピッツ発振回路の開ループの伝達特性の周波数特性から考える。このことはあまり書かれたものを見たことがない。

図には書いてないが、R1をVin端子のIN抵抗、R3をC2に並列な抵抗とする。このR1、R3がない場合は、
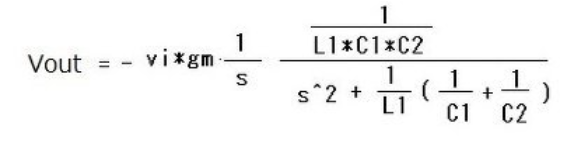
----(1)
になる。R1、R3がある場合、

---(2)
という置き換えを(1)式にすればいい。
すると、

---(3)
となる。

ここでR1-->∞とすれば次のようになる。

---(4)
発振条件はこの式で、
位相=0
ゲイン>=1
である。
位相=0
分母の虚数部=0
ーjω0^3*L1C1C2R2+jω0(R2C2+R2C1)=0
ω0^2*L1C1C2=(C2+C1)
ω0=√((C1+C2)/(C1C2L1))
ゲイン>=1
ーgm(R2/L1)/(-ω0^2C1L1+1)
=ーgm(R2/L1)/(-((C1+C2)/(C1C2L1))C1L1+1)
=gmR2(C2/C1)>=1
http://www.mogami-wire.co.jp/puzzle/pzl-04.html
http://www.zuken.co.jp/club_Z/z/analog/006/ana_110120_1.html
もし、水晶発振子のようにLに並列にC3が入っていれば、(1)式で
1/L1-->1/L1+s^2*C3
という置き換えをすればいい。

---(5)
であるから、
ω0=√(1/(L1*(C1//C2+C3)
さらにL1に直列にC4が入っていえば(5式で、
L1-->L1+1/(s^2*C4)
と置き換えればいい。C1//C2をC12と書けば、

---(6)
となる。
発振角周波数ω0は、

ー--(7)
