ライター：mpcsp079さん（最終更新日時:2016/10/7）投稿日：2016/1/4

対称座標法を簡潔に解説

対称座標法の基礎回路 | 音声付き電気技術解説講座 | 公益社団法人日本電気技術者協会 (jeea.or.jp)

対称座標法を簡潔に解説してみた。この方法は、

①

対称性がなくなったため、簡易的な計算が不可能になった回路を、対称（平衡）成分に分解することによって、１相分の計算で済むようにするアイデアである。

②

さらに、送電線路によるインピーダンス行列を対角化し、零、正、逆のかく成分を完全に分離して考えられる。

という利点がある。

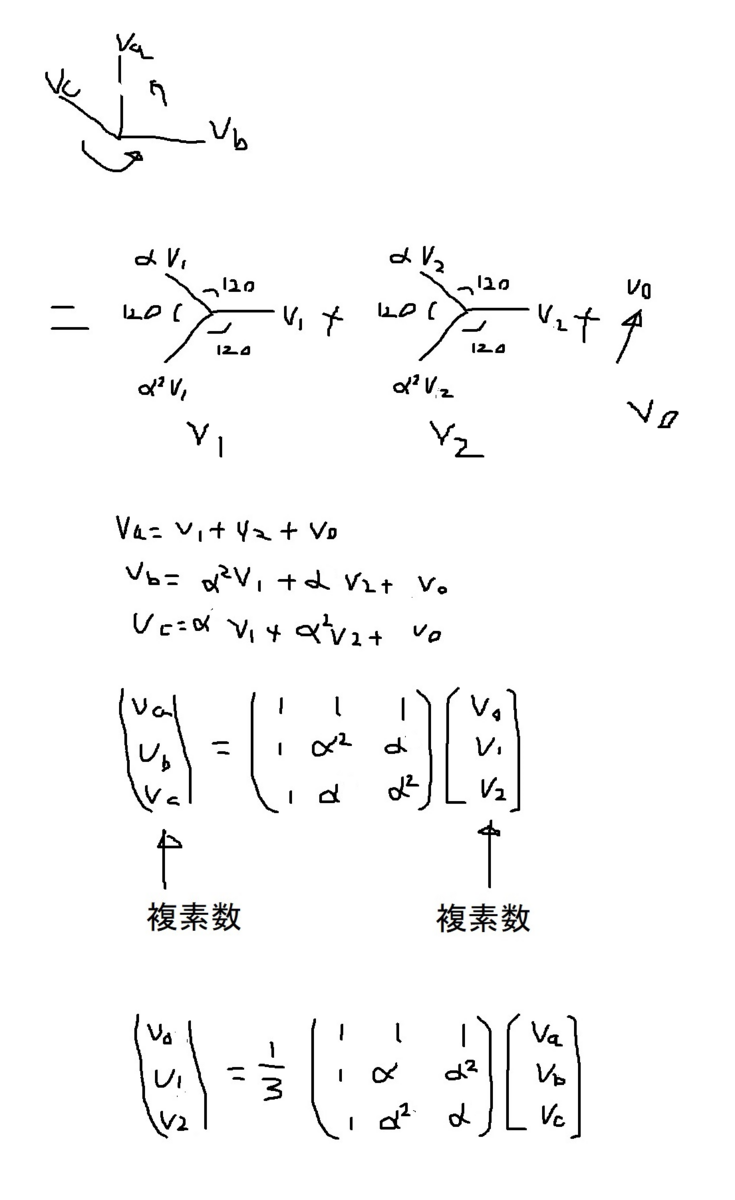
■非平衡３相フェイザ（電圧、電流）の平衡フェイザへの分解

　　　　　　　　　図１　分解されるべき非平衡３相フェイザ

　　図１のような非平衡なフェイザを、図２の２つの平衡３相フェイザＡ，Ｂ，Ｃ，ａ，ｂ，ｃと１つの単相フェイザＤの和で表そうということです。
　　　ｆ＝Ｄ＋Ａ＋ａ
　　　ｇ＝Ｄ＋Ｂ＋ｃ
　　　ｈ＝Ｄ＋Ｃ＋ｂ　

　Ｄ＝（ｆ＋ｇ＋ｈ）／３

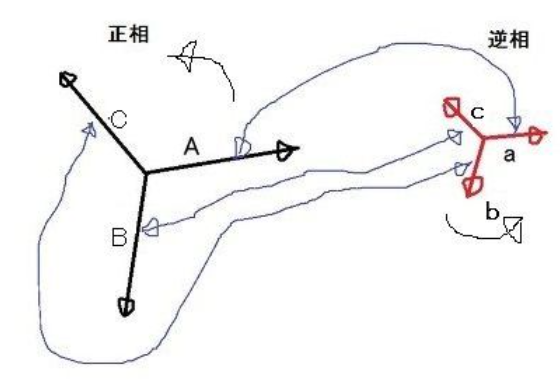
　　　　　　　　　図２　２つの平衡３相フェイザ

参考でちゅ
http://www.jeea.or.jp/course/contents/01123/

　　どうしてこんなことができるか証明します。下図が対称座標で表すべき３相（ｆ，ｇ，ｈ）のフェイザです。これを２つの平衡３相フェイザＡ、Ｂ，Ｃとａ，ｂ，ｃと単相フェイザＤで次のようになるとします。
　　　ｆ＝Ｄ＋Ａ＋ａ
　　　ｇ＝Ｄ＋Ｂ＋ｃ
　　　ｈ＝Ｄ＋Ｃ＋ｂ　　　　

　　ここでαを単位長で偏角１２０°のフェイザとしますと
　　　Ｂ＝α＾２＊Ａ
　　　Ｃ＝α＊Ａ
　　　ｂ＝α＊ａ
　　　ｃ＝α＾２＊ａ
となり、
　　　ｆ＝Ａ＋ａ＋Ｄ
　　　ｇ＝α＾２＊Ａ＋α＊ａ＋Ｄ
　　　ｈ＝α＊Ａ＋α＾２＊ａ＋Ｄ
となり、これはＡ，ａ，Ｄに関する連立方程式であり、これを解くことで求まります。係数の行列式は≠０なので解は存在します。

　　つまり、

　　　単相フェイザＤ
　　　正相３相フェイザＡ，α＾２＊Ａ、α＊Ａ
　　　逆相３相フェイザａ，α＊ａ，α＾２＊ａ
　　　
が求まります。

　　つまり、不平衡フェイザｆ，ｇ，ｈが２つの３相平衡フェイザと１つの単相フェイザで表されたことになります。
これで証明終わりです。

　　正相分と逆相分はどちらも反時計まわりです。フェイザはすべて同じ方向に回転していなければなりません。ことなる回転方向のフェイザをたすことは意味ありません。

■使用法 １

http://www.jeea.or.jp/course/contents/01125/

　　　　　　　　　　　　　　　　図７

　　Ｅａ，Ｅｂ，Ｅｃ，Ｖａ，Ｖｂ，Ｖｃ，Ｉａ，Ｉｂ，Ｉｃについて次の方程式が成り立つ。送電線間に相互インダクタンスや容量などがある場合、それらは対称であるとしれば、インピーダンス行列は対角要素はすべて等しく、かつ非対角要素も等しくなる。

ここで、

Z0=z1+2z2+3Rn

Z1=z1-z2

Z2=z1-z2

とし、零相、正相、逆相インピーダンスという。これらより、

　　　０＝Ｖ０’＋Ｚ０＊Ｉ０

　　　Ｅａ＝Ｖ１’＋Ｚ１＊Ｉ１

　　　０＝Ｖ２’＋Ｚ２＊Ｉ２

となる。

■使用法２

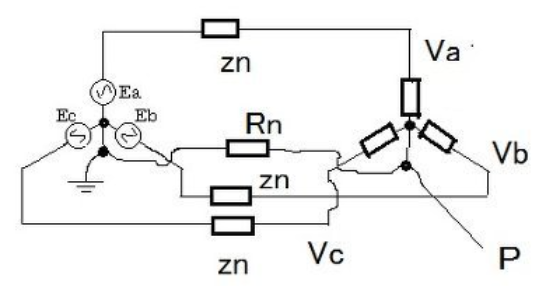
　　　　　　　図８　　不平衡負荷による不平衡電流、電圧

　　図７において電源は平衡であるとする。Ｖａ，Ｖｂ、Ｖｃ、Ｉａ，Ｉｂ，Ｉｃは平衡ではない。そこで、
　　　　Ｖａ＝Ｖ０＋Ｖ１＋Ｖ２

　　　　Ｖｂ＝Ｖ０＋α＾２＊Ｖ１＋α＊Ｖ２

　　　　Ｖｃ＝Ｖ０＋α＊Ｖ１＋α＾２＊Ｖ２
　　　　Ｉａ＝Ｉ０＋Ｉ１＋Ｉ２

　　　　Ｉｂ＝Ｉ０＋α＾２＊Ｉ１＋α＊Ｉ２

　　　　Ｉｃ＝Ｉ０＋α＊Ｉ１＋α＾２＊Ｉ２

と対称座標で表せる。また、
　　　　Ｉ０＝（Ｉａ＋Ｉｂ＋Ｉｃ）／３

　　　　Ｉ１＝（Ｉａ＋α＊Ｉｂ＋α＾２＊Ｉｃ）／３

　　　　Ｉ２＝（Ｉａ＋α＾２＊Ｉｂ＋α＊Ｉｃ)／３
ともかける。

　　　　Ｖ０＝－Ｚ０＊Ｉ０

　　　　Ｖ１＝Ｅ－Ｚ１＊Ｉ１

　　　　Ｖ２＝－Ｚ２＊Ｉ２
ここで、ａ相地絡、つまり、ＺＢ，ＺＣ＝∞、ＺＡ＝Ｒｇとする。

　　すると、Ｉｂ＝Ｉｃ＝０、Ｉａ＝Ｉｇ、だから、上の式から、

　　　　Ｉ０＝Ｉ１＝Ｉ２＝Ｉｇ／３＝Ｉａ／３

が成り立つ。また、各平衡成分ごとに次が成り立つ。　　　

　　　　Ｖ０＝－Ｚ０＊（１／３）Ｉｇ

　　　　Ｖ１＝Ｅ－Ｚ１＊（１／３）Ｉｇ

　　　　Ｖ２＝－Ｚ２＊（１／３）Ｉｇ

Ｖａは地絡であるから、
　　　　Ｖａ＝Ｖ０＋Ｖ１＋Ｖ２＝０

だから、

　－Ｚ０＊（１／３）Ｉｇ＋　Ｅ－Ｚ１＊（１／３）Ｉｇ－Ｚ２＊（１／３）Ｉｇ＝０

　　Ｉｇ＝３Ｅ／（Ｚ０＋Ｚ１＋Ｚ２）＜－－－答え
　　では、Ｚ０，Ｚ１，Ｚ２はどのように出てくるか？

http://energychord.com/children/energy/trans/tl/contents/tl_sym_coord_app.html

から引用する。

　　相互に作用しあう送電線を考える。

送電線の端間電圧⊿Ｖａ，⊿Ｖｂ、⊿Ｖｃと電流Ｉａ，Ｉｂ、Ｉｃの関係は、

となる。

　　これをこれを零相、正相、逆相に分解すると、

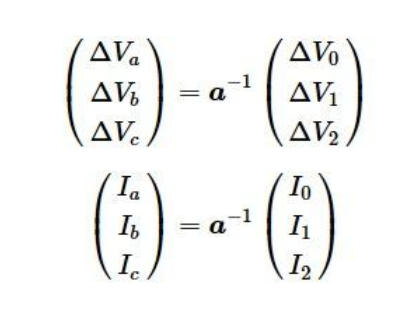
となり、さらに、

と対角化され、

となる。

　　つまり

　　　　Ｚ０＝Ｚ１１

　　　　Ｚ１＝Ｚ２２

　　　　Ｚ２＝Ｚ３３、

となる。

■参考質問

至急です！電気回路の問題です！三相の非対称電流を対称電流に変換し、零相電... - Yahoo!知恵袋

至急です！電気回路の問題です！
三相の非対称電流を対称電流に変換し、零相電流、正相電流、逆相電流をそれぞれ求めなさい。
Ia＝j[A]
Ib＝1[A]
Ic＝-1[A]

解答

ｊ＝Ａ＋ａ＋Ｄ
１＝α＾２＊Ａ＋α＊ａ＋Ｄ
ー１＝α＊Ａ＋α＾２＊ａ＋Ｄ
α＝ｅ＾（ｊ２π／３）
から、
Ｄ＝（ｊ＋１－１）／３＝ｊ／３
すると、
ｊーｊ／３＝２ｊ／３＝Ａ＋ａ
１ーｊ／３＝α＾２＊Ａ＋α＊ａ
となり、
２ｊ／３＝Ａ＋ａ
（１ーｊ／３）／α＝α＊Ａ＋ａ
から、
２ｊ／３ー（１ーｊ／３）＝Ａーα＊Ａ
ゆえに、
Ａ＝（２ｊ／３ー（１ーｊ／３））／（１－α）
ａ＝２ｊ／３ー（２ｊ／３ー（１ーｊ／３））／（１－α）