変圧器の解析

変圧器の理解の仕方、処理の仕方には2つある。これを整理してみた。

図1 変圧器モデル
■変圧器の構成
図1において、コイル1と2が高透磁率のコアに巻いてある。簡単のためにコイルは同一場所に巻いてあり(つまり広がりがなく)、巻き数はN1,N2とする。コイル1を1ターンとしたときの電流1Aによるコイル1中の磁束Φ1のうち、コイル2を通る部分をΦ12とする。おなじく、コイル2を1ターンとしたときの電流1Aによるコイル2中の磁束Φ2のうち、コイル1を通る部分をΦ21とする。コイルを通るとは、コイルの部分を通る磁束であり、巻き数は関係なくコイルの巻いてある部分をを通るものを考える。相反性から、
ΦM=Φ12=Φ21 ---(1)
ここで、変圧比N1/N2=V1’/V2’をaとすることを覚えていてもらいたい。
相反定理は次を参照
http://qube.phys.kindai.ac.jp/users/kondo/lectures/em_tb/node195.html

図2 変圧器モデル
そこで、これらの結果より変圧器の等価回路を図2の(b)のように考える。L1’,L2’は漏れインダクタンスと言われる。LX1,2の上の点は、それが同じ方向にあるとき、Mが正であることを示す。つまり、図2の状態において、V1’によって生じる磁束ΦMによって生じるV2’は、図の位置でV1’と同相であるということだ。もし、この点が互い違いに打ってあれば、V1’とV2’が逆相であることになる。Mで言えば、これが負になるのである。
LX1=L1+L1’
LX2=L2+L2’
L1’,L2’は漏れインダクタンスという。
L1=Φ12*N1^2=ΦM*N1^2 ---(2)
L1’=(Φ1-Φ12)N1^2=(Φ1-ΦM)N1^2 ---(3)
L2=Φ21*N2^2= ΦM*N2^2 ---(4)
L2’=(Φ2-Φ21)N2^2=(Φ2-ΦM)N2^2 ---(5)
M=Φ12*N1*N2=Φ21*N1*N2 ---(6)
=ΦM*N1*N2=√(L1*L2) ---(7)
■第一の等価回路(T型等価回路)
これは回路理論で出てくる。完全な数学的な扱いである。
図2(a)のT型等価回路を4端子パラメータ論により、エレガントに考えてみる。この等価回路は、無条件に機械的に成立し、漏れインダクタンスなど理解する必要はない。もっとも簡単で論理的な等価回路ではあるが、変圧器の理解は深まらない。
より考える。
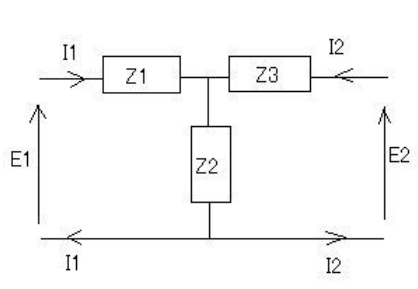
図3 T型回路
図2(a)より、
V1=jωLX1*I1+jωM*I2 --(8)
V2=jωLX2*I2+jωM*I1 --(9)
図3では、
V1=(Z1+Z2)*I1+Z2*I2
V2=Z2*I1+(Z2+Z3)*I2
となるから、ここで
X1=jωLX1
X2=jωLX2
X3=jωM
とおくと、
Z1+Z2=X1
Z2=X3
Z2=X3
Z2+Z3=X2
となるので、
Z2=X3=jωM
Z1=X1-X3=jω(LX1-M)
Z3=X2-X3=jω(LX2-M)
という関係があれば、図4は(8)(9)式の関係が成り立っている。この場合、LX1、LX2,Mの間には制約はない。変圧器の極性が逆である時は、Mを負にすればいい。図7の各インダクタンスは負の値もあり得る。あくまでも数学モデルである。
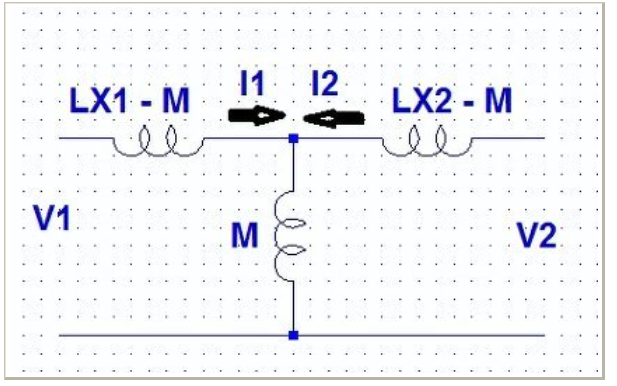
図4 式(14)(15)を実現するT型回路
もし、巻き方が 逆極性であれば、つまり、LX1,2の点が互い違いであるならば、Mが負になる。これを正の数MによりーMと表せば、図5のようになる。-Mというインダクタンス(Mは正)は現実にはない。つまり、この回路は実現はできない。つまり、この回路をT型回路で実現することはできない。しかし、IN/OUT間の関係は、図2(a)と同じなのである。単なる数学的なモデルである。
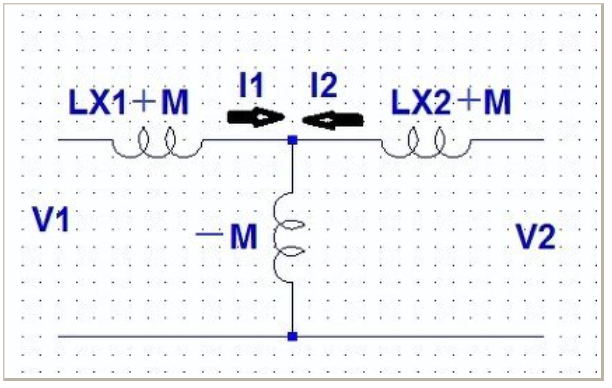
図5 逆極性の場合のT型等価回路
■第二の等価回路(電気機器学でやる考え方)
http://ja.wikipedia.org/wiki/漏れインダクタンス
これは電気機器学で出てくる。実際の動作から考えられている。上の等価回路のような非現実なものは出てこない。
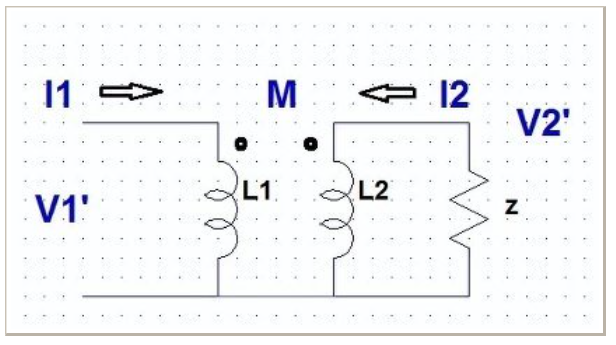
図6 もれ磁束なし変圧器
電気機器学では次のように説明される。図6、つまり図2(b)でL1’、L2’がない場合で考える。この場合、L1を通る磁束はすべてL2も通る。逆も成り立つ。
まず、負荷Zがない場合、コイル1の磁束ΦM=Φ12=Φ21による電圧が1次側電圧V1’に釣り合う。
V1’=jωΦM*N1
より、
ΦM=V1’/(jω*N1)
このΦMによる2次側の電圧V2’は、
V2’=jωΦM*N2=jω*N2*V1’/(jω*N1)
=N2*V1’/N1
V2’/V1’=N2/N1
そして、このときI1は、
I1=V1’/(jωL1)=V1’/(jωΦM*N1^2)
が流れる。これを一般にはI0と書き、励磁電流という。
このとき、
L1*I1=L2*I2=ΦM
L1=A*N1^2
L2=A*N2^2
L1/L2=(N1/N2)^2
ここで、負荷Zをつなげて2次電流I2が流れたとする。この電流I2により、磁路の磁束は変化する。すると誘起電圧がV1’と釣り合わなくなるので、ほぼ瞬間的に1次側からこれを打ち消すために1次電流が流れる。起磁力の釣り合いから、これは次の関係を満足しなければならない。
I1負荷*N1=I2*N2
つまり、
I1負荷=I2*N2/N1
となる電流が、I0に追加されることになる。そこで1次電流I1は、
I1=I0+I1負荷
となる。この等価回路は図7となる。
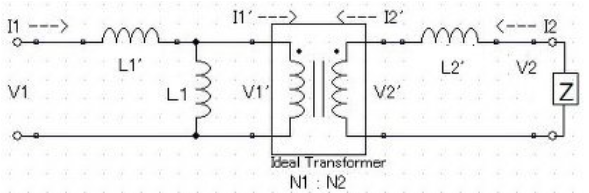
図7 変圧器の等価回路
ここで、理想変圧器とは、励磁電流がいらなく、電圧比がN1:N2、電流比がN2:N1の仮想素子(機器)である。 つまりV1’を加えたとき、V2’=V1’*N2/N1となり、I2’が流されるとI1’=I2’*N2/N1が流れるという、架空の装置なのである。
変圧比N1/N2=V1’/V2’をaとし、V1とI1の関係のみに注目すると、図7はさらに図8になる。この図は、1次側の電流 I1のみが元回路と等価なのである。
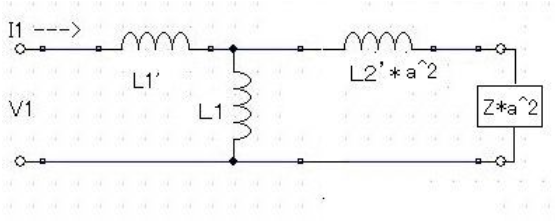
図8 1次側に換算した等価回路
ーーーーーーーー おわり ーーーーーーーーーーー

参考
http://www.electrical4u.com/equivalent-circuit-of-transformer-referred-to-primary-and-secondary/
http://simcir.co.jp/Circuit_Theory/Mutual_Induction.html
=========以下保留============
■図3にもれ磁束がない部分のみを示す。この部分を解析する。
V1’=jωL1*I1+jωM*I2 --(8)
V2’=jωL2*I2+jωM*I1 --(9)
端子2に抵抗Zがついていると、
V2’=-I2*Z ---(10)
(9)式に入れ、
-I2*Z=jωL2*I2+jωM*I1
I2(-Z-jωL2)=jωM*I1
I2=jωM*I1/(-Z-jωL2)
これを(8)式に入れ、
V1’=jωL1*I1+jωM*jωM*I1/(-Z-jωL2)
I1=V1’/(jωL1+jωM*jωM/(-Z-jωL2))
=V1’*(-Z-jωL2)/(ーjωL1*Z+ω^2L1L2ーω^2M^2)
(2)(4)(6)(7)から、
L1*L2=M^2であるから、
I1=V1’*(Z+jωL2)/(jωL1*Z) ーーー(11)
I1=V1’*(1/jωL1+L2/(L1*Z))
=V1’*(1/jωL1+N2^2/(N1^2*Z)) ーー(11)’
一方(8)(9)式から、
L2*V1’=jωL1L2*I1+jωM*L2*I2
M*V2’=jωL2*M*I2+jωM^2*I1
となり差をとると、この場合、L1*L2=M^2であるので、
L2*V1’ ー M*V2’=I1(jωL1L2ーjωM^2 ) =0
V2’/V1’=L2/M=√(L2/L1)=N2/N1 ---(12)
ーーーーーーーーー
L2=L1/a^2
であるから、
Za=Z*a^2
と置くと、
I1=V1’*(Za/a^2+jωL1/a^2)/(jωL1*Za/a^2)
= V1’*(Za+jωL1)/(jωL1*Za) ーーー(13)
となり、これは図4のような等価回路になる。
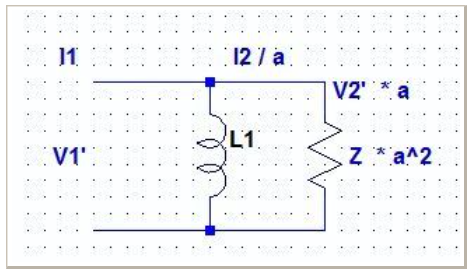
図4 式(13)に対応する等価回路
この図4は1次側の電圧、電流に関しては図3と等しいが、2次電圧は異なる。つまり、1次側に換算された等価回路なのである。この場合、つまり、図2において、N1=N2として、他の定数を次のように変換した場合に等しい。
L1=ΦM*N1^2
L2ーー>L2a=ΦM*N2^2*a^2=ΦM*N1^2=L1
L1’=(Φ1-ΦM)N1^2 =Φ1*N1^2-Ma
= LX1-Ma
L2’ーー>L2a’=L2’*a^2=(Φ2-ΦM)N2^2*a^2
=(Φ2-ΦM)N1^2 =Φ2*N1^2-Ma
=LX2*a^2-Ma
Mーー>Ma=M*a=ΦM*N1*N2*a=ΦM*N1^2
これを図5に示す。これが良く出てくる図である。図4のZは、図5から、
Z=LX2-M/a+ZL
となる。
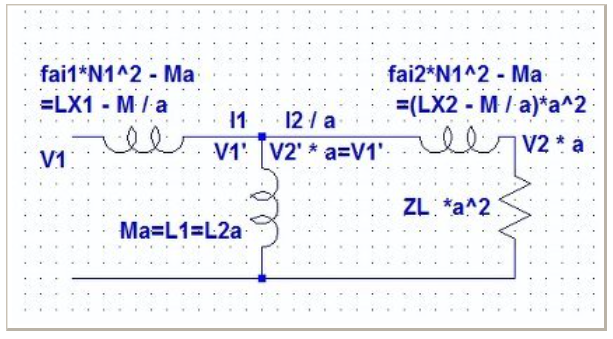
図5 図2を1次側に換算した等価回路