❤オペアンプ　OPAMP　ＬＭ３２４位相補償解析

ライター：mpcsp079さん（最終更新日時:2016/4/16）投稿日：2013/5/14

ＬＭ３２４の位相補償とＦ得を調べた

　　　　　　　　　図1　ＬＭ３２４ＯＰＡＭＰ回路

　　　　　　　　　　　　図2　図1の簡略化回路

図２－補足　実際はＱ９が入り、Ｑ６のベース電圧を調整します。

　　　　　　Ｑ６のＶｂｅを０．６５Ｖにするためです。

　　　　　　　　　　　図3　さらなる簡略化回路

図3において、ＢＪＴの等価回路でのrb,rπ,rπ、Cμ（図ではrpi,Cpi、Cu とした）をＢＪＴの外に示した。したがって図のＢＪＴは入力インピーダンス無限である。Cu（Ｃμ）はコレクターベース間容量であり、Ｃｃは位相補償容量である。

　　　　　　　　　図4　エミッタフォロワ省略

図４において、ＲＬ１、ＲＬ２は図３のエミッタフォロワの入力インピーダンスとしていて、周波数特性や後段からの影響を無視している。同じように、図3のエミッタフォロワの出力インピーダンスを０として、その周波数特性と値を無視している。これにより、前後段が分離して計算が簡単になる。

http://note.chiebukuro.yahoo.co.jp/detail/n178570

によれば、エミッタフォロワの周波数特性はωＴ（β＝１となる周波数）まで一定であるという結果がでているし、この値は１０ＭＨｚ以上であると考えられるので、このＯＰＡＭＰの帯域が１ＭＨｚであることから考え無視しても妥当であると言える。

　　　　　　　　　　図5　帰還容量をミラー容量に置き換える

　　図5ではすべての帰還容量（Ｃμ、Ｃｃ）をミラー容量に変換して近似回路としている。帰還部分がなくなったので計算が容易になる。それでもミラー容量はそのアンプのゲインが反映されるので、後段から決めていかなくてはならない。

　　　　　　　　　　図6　図5の小信号等価回路

　　図6は図5の小信号等価回路である。

http://note.chiebukuro.yahoo.co.jp/detail/n178297

の式（３）により、

　（２）式の中のＣ３は（１）式で定められたものであり、（３）式の中のＣ２は（２）式で定められたものであることが注意である。つまり、きわめて複雑な式となる。

viからvo間での伝達関数は、

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（４）　

となる.。すべての項は掛け算である。Ｃ１，Ｃ２，Ｃ３も詳細に書くと、

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（４）’

となり、きわめて複雑です。このＣ１，Ｃ２，Ｃ３を（４）’式のように代入すると大変なことになります。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（５）

　結局（５）式のように近似できる。（３）式などによれば、Ｔ１はＣπ＊rｂ程度になるようなので極、ー１／Ｔ１はゲイン＝１の周波数（１ＭＨｚ）に比べはるかに高い周波数となるとよそうされる。そこで帯域内では、

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（５）’

と近似できる。これは帯域内では位相は―90°となりどんな帰還率でフィードバックしても安定になる。（５）’式は正確に書けば、

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（６）

である。極ー１／(CcR)は非常に低くなっている。

　＊＊＊＊　勉強会　＊＊＊＊

　使う知識は交流理論、トランジスタ等価回路のみであり、ラプラス変換はいりません。がんばれば理解できるはずです。

　　＊＊＊＊＊　計算の基礎　＊＊＊＊＊＊＊

①　ＲとＣが直列の場合、そのインピーダンスＺは？

　　　　V/I=Z=R+1/(jωC)

である。これからはｊωをｓとおきます。つまり、

　　　　V/I=Z=R+1/(sC)

と書きます。これはＩからＶへの伝達関数でもありますが、ラプラス変換を知らなくてもだいじょうぶで、単にｊωをｓに置いただけと考えてもいいです。最後の結果においてｓ－－＞ｊωと置き換えればいい。

②抵抗ＲのインピーダンスはＲ

③容量Ｃのインピーダンスは１／（sC)

④インダクターＬのインピーダンスはｓＬ

⑤ＲとＣの直列回路のインピーダンスはＲ＋１／（ｓＣ）

⑥ＲとＣの並列回路のインピーダンスは（R*(1/(sC))/(R+(1/(sC))=R/(1+sCR)

これＯＫかな？Ｒ１とＲ２の並列抵抗はＲ１＊Ｒ２／（Ｒ１＋Ｒ２）ですね。

⑦インピーダンスＺに電流Ｉを流した時のＺにかかる電圧Ｖは、

　　　　　　Ｖ＝Ｉ＊Ｚ

⑧電圧の分圧。

　　　　　　　　　　　図7

図のような場合、Vo=Vi*Z2/(Z1+Z2)

　　　＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

　　　　　＊＊＊＊＊　　軽く計算例　　＊＊＊＊＊＊

⑨エミッタコモン回路

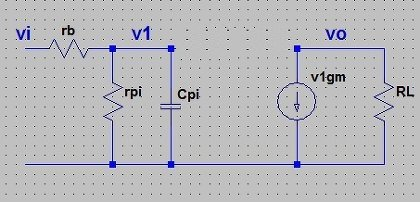
　　　　　　　　　　　　　　　　図8

V1=Vi*(rpi//Cpi)/(rb+(rpi//Cpi))

vo=-v1gmRL （－がつくのは電流源記号の矢印が下向きだから）

　　　　∴　vo=-vi*gm*RL*(rpi//Cpi)/(rb+(rpi//Cpi))　　　　　　　　　　　(a1)

ここで、

　　　　　rpi//Cpi＝rpi/(1+s*rpi*Cpi) 　ですね！ (a2)

⑩コレクターベース間容量Ｃμの処理

　　　　　　　　　　　　　　　図9 　　

　　この回路はＣμによりフィードバックされているので計算がやっかい。そこで下の⑪のようにミラー容量を考え、ＩＮ／ＯＵＴを分離する。等価なものではなく、近似であるところ注意！

http://note.chiebukuro.yahoo.co.jp/detail/n180115

参照

⑪ミラー容量近似

　　　　　　図10

ゲイン=G＝vo/vi

とすると、

Ｃ１＝Cpi+(1+G)*Cu

である。図では、

Ｃ１＝Cpi+(1+gmRL)*Cu

もしRLが容量Ｃであれば、

　Ｃ１＝Cpi+(1+gm1/（ｓＣ）)*Cu

⑨の(a1)式のCpiをC1に置き換えればvo/viが計算できる。

これは

http://note.chiebukuro.yahoo.co.jp/detail/n178297

の（３）式である。

　＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

追加

⑫

それから、下の図の場合電流ｉ１，ｉ２は？

　i1=Z2/(Z1+Z2)　

　i2=Z1/(Z1+Z2)

ですね。証明は、

図の並列インピーダンスＺは

Ｚ＝Z1*Z2/(Z1+Z2)

ですね。この電圧はＺ＊ｉですね。するとＺ１の電流 i1 は、

i1=(i*Z1*Z2/(Z1+Z2))/Z1=i*Z2/(Z1+Z2)

i2=(i*Z1*Z2/(Z1+Z2))/Z2=i*Z1/(Z1+Z2)

　－－－－－－　　2012　 5　　 18　－－－－－－－

このままでは分かりずらいので紙にでも図と式をかきながらやってくだされ。

　＊＊＊＊＊　極について＊＊＊＊＊＊

ここで休憩して、極の話をします。図８の回路を２つつなげたとします。つまり、RLのかわりに同じ回路がつながるのです。このときのvo/viを計算しましょう。ここで２段目のrpi,Cpiをrpi2,Cpi2として１段目と区別します。このとき２段目のv1もv12として区別します。

v12=（1段目から流される電流のうちCpi2に流れる電流)＊（Cpi2のインピーダンス)

　　=(1段目から流される電流)*(rpi2/(rpi2+1/(sCpi2))*1/(sCpi2) (a3)

2段目のvoは、

vo=-v12*gm*RL

となる。わかりますか？Ｚ１とＺ２の並列回路に電流Ｉが流されたときＺ２に流れる電流Ｉ２は、

Ｉ２＝Ｉ＊Ｚ１／（Ｚ１＋Ｚ２）

となります。どうしてかわかりますか？　(a3)ではＺ１＝rpi2、Ｚ２＝1/(sCpi2)ですね。

そこで(a1)から 1段目のRＬに流される電流は

-vi*gm*(rpi//Cpi)/(rb+(rpi//Cpi))　　　(a4)

（a3)から、この電流に、

　(rpi2/(rpi2+1/(sCpi2))*1/(sCpi2) (a5)

をかけたものがv12となり、これに

gm*RL (a6)

をかけたものがvoとなる。つまり、

vo=(a4)*(a5)*(a6)

となる。この結果を整理すると、

となる。位相は１つの極でー９０°となりますから、２つあると最終的にー１８０°動きますね。もう少しかんがえてみましょう。　わかりやすくするため、-p1<<-p2とします（絶対値でp2が大きいという意味)。　ｓ＝ｊωとして周波数応答を考えます。　(a8)を見ましょう。　

ｊで割るということは位相がー９０°であるということ。ｊ＾２つまりー１で割るということはー９０－９０＝－１８０°であるということ。

と各領域で近似できます。これをグラフに書くと ωが-p1を過ぎると２０ｄＢ／ｄｅｃで下降し、さらに-p2を過ぎると４０ｄＢ／ｄｅｃで下降する形になります。つまり、周波数ωが極を通過するごとに位相は９０°づつ遅れていきます。ＯＰＡＭＰでは多段になりますから、極は５個かそれ以上できます。つまりそのままではフィードバックして使えないことになります。

　　下に紹介したＵＲＬの資料ｐ１０の図がわかりやすい。

　＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

　＊＊＊＊＊　交流理論について　＊＊＊＊＊

ある周波数ｆ（角周波数ω＝２πｆ）で電圧電流がある場合、すべては角周波数ωの正弦波である場合、未知なものはその振幅と位相である。この関係を複素数を使って簡単に計算できるようにしたものが交流理論である。Ｖ／Ｉはインピーダンスという。その他電圧同士の関係など。値は振幅と位相情報をもつ。同じ角周波数で動く量の関係のみ（振幅と位相差）を計算しようとするため、時間変化の項（ｓｉｎ（ωｔ）、正確に言えばｅ＾（ｊωｔ））は省かれている。

Ｒ，Ｃ，Ｌは上のようにＲ，１／ｓＣ、ｓＬとして普通の抵抗計算と同じように計算できる。結果は複素数の大きさと位相角がでてくるし、ωをかえれば周波数によりそれらがどう変化するかがわかる。

これがわかっているかなあー？？？　むずかしいですよ。

　＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

　＊＊＊＊＊　ざっとした見方の重要性　＊＊

　＊＊＊＊　要素3の完全な解析です　＊＊＊

　（４）’式は複雑であるが、まずつぎのようなおおざっぱな理解が大事である。そうしてから（４）’式のような詳細な検討に進むことが好ましい。どうして（５）’（６）式のようになるのか説明します。

　少し難しくなるがどうしてこうすると、極が帯域外にいってしまうのかを説明する。ラプラス変換は関係なく、交流理論だけで理解できますよ。

　－－－－－－－－－追加文章ーーーーーーーーーーーーー

　　ここでは上のようにな伝達特性の式の分母を因数分解して極を求めるのではなく、その周波数特性の変化点から極を推測していこうとするものです。因数分解は現実に不可能だし、この方が大きな見通しを得るのにいいのです。

　－－－－－－－－－－－－－－－－－－－－－－－－－－

　　　　　　　図１１　ＯＰ　ＡＭＰの位相補償ブロック図

　図１１において、要素１は初段差動部分のベース部分。要素２はそのコレクタ部分。要素３は位相補償部分である。要素１はポールｐ１をもつ。このｐ１はｃ点からみた要素３の入力インピーダンスに依存する（ミラー容量のため）。要素２はｖ１に従属した電流源である。要素３は入力にエミッタフォロワをいれてあるエミッタコモン回路であり、入力インピーダンスが高い。また負荷としては電流源と出力段（不図示）のエミッタフォロワなので電圧ゲインは大きい。しかし、負荷インピーダンスが大きいため、ミラー効果で低い周波数にポールができてしまっている。Ｂはこの特性を表している。つまりＢには低いポールがある。当然問題にならない高い周波数のポールも持っている。

図１２　要素３の詳細

　まず要素３から考える。図１２において考察する。Ｚ１は要素２のＯＵＴ側から見たインピーダンスと要素3の入力インピーダンスの並列値、Ｚ２は１／ｓＣｃである。ｉは要素２の電流ＯＵＴである。これからｉからｖｏまでの伝達特性を考える。

ve=i*Z1*Z2/(Z1+Z2) + vo*Z1/(Z1+Z2)

vo=-ve*B

　＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

上のはじめの式は重ねの理で計算した。つまり

①vo=0　でvo点をＧＮＤにショートし、　ｉ　のみ存在するときのveの値と、

②ｉ＝０でvoのみ存在する場合のveの値を

合計したものである。

　＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

これらよりveを消去すると、

-vo/B=i*Z1*Z2/(Z1+Z2) + vo*Z1/(Z1+Z2)

-vo*(1/B+Z!/(Z1+Z2))=i*Z1*Z2/(Z1+Z2)

vo=-i*Z1*Z2*B/(Z1+Z2+Z1*B)

=-i*(Z1*Z2/(Z1+Z2))*(B/(1+B*Z1/(Z1+Z2)))　　　　　(a9)

ここで式（a9)の　B/(1+B*Z1/(Z1+Z2))　　考える。Ｂはエミッタフォロワも含むから多くのポールをもつ。しかし、それが

ＯＰＡＭＰの帯域内をだいぶ超える周波数領域で十分なゲイン（＞＞１）をもつならば、　

この部分の分母は≒B*Z1/(Z1+Z2)と近似できる。すると(a9)式は、

voi≒-i*(Z1*Z2/(Z1+Z2))*(Z1+Z2)/Z1=　-i*Z2　　　　　　(a10)

と簡単になってしまう。つまり、いくらＡＭＰのＢにＯＰＡＭＰ帯域内にポールがあっても、十分ゲインが大きければ、Ｃｃ　によるフィードバックにより、帯域外に追い出すことができるのである。十分周波数がおおきくなれば、多くのポールがでてくるので（a10)は成り立たなくなる。ここで、

Ｚ２＝１／（ｓＣｃ）

とすると、ｓ＝ｊωとして周波数をーー＞０にしてゆくと、Ｚ２は大きくなってゆく。すると上で考えた

B/(1+B*Z1/(Z1+Z2))の分母は今度は≒１　となってしまう。さらに

Z1*Z2/(Z1+Z2)　はＺ２－－＞大　で　－－＞Ｚ１になってゆく。つまり周波数は低くなると、

vo≒=-i*Z1*Ｂ　　（低周波）

になる。この切り替わり周波数が低域のポールとなる。

さらにこの部分の入力インピーダンスＺｉｎを考える。

上の式

ve=i*Z1*Z2/(Z1+Z2) + vo*Z1/(Z1+Z2)

vo=-ve*B

で、voを消去すると、

ve=i*Z1*Z2/(Z1+Z2) -ve*B*Z1/(Z1+Z2)　　　　　

Ｚｉｎ=ve/i=(Z1*Z2/(Z1+Z2))/(1+ B*Z1/(Z1+Z2)) (a11)

ここで 1<< B*Z1/(Z1+Z2) であるような周波数では(a11)は次のようになる。

Ｚin≒Z2/B (a12)

つまり、

Ｚｉｎ≒1/(jωCc*B) (a13)

となり、ＢがおおきいとＺｉｎは小さくなる。すると図１１の要素１のミラー容量は小さくなり、これによるポールは帯域外になると思われる。つまりＯＰＡＭＰ帯域内では、(6)式のような簡単なものになることがわかった。

　　＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

　　＊＊＊＊＊＊　まとめ　＊＊＊＊＊＊＊＊＊＊

　　(a13)式はミラー効果の証明になっている。ゲインーＢのアンプにＣｃでフィードバックすると、ＩＮ側から見るとＣｃ＊Ｂの容量に見えるということの完全な証明だ。

　　図11の要素３に関する(a9)式、

vo=-i*(Z1*Z2/(Z1+Z2))*(B/(1+B*Z1/(Z1+Z2))　　　

の分母　

　　　　　　1+B*Z1/(Z1+Z2)

は、Ｂのポールの数がｎなら、つまりＢがｓのｎ次多項式なら、ｎ次以上の多項式になる。これを因数分解したものがポールである。　上での考察により、(a9)のポールは非常に低い周波数が１つと、残りは高い周波数になることがわかった。それは、周波数特性がその高い周波数まで平らだからである。つまり、Ｂのポールが低い側と高い側に移動したと考えられる。下の資料ｐ２６に示されている。

　　＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

参考に

http://www.si.eei.eng.osaka-u.ac.jp/reference/osk_0208_03.pdf#search='位相補償'

かなりおおざっはですがいろいろ説明されています。ちらりと眺めるだけにして。

　　＊＊＊＊　５／２１　参考までに＊＊＊＊＊

簡単な例で極移動を計算してみました。

http://note.chiebukuro.yahoo.co.jp/detail/n179936

こんな質問もありました。

http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q14107618614

回答です。

http://note.chiebukuro.yahoo.co.jp/detail/n180115

　　　　　＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊