ロケットの姿勢制御と慣性モーメント
ライター:mpcsp079さん(最終更新日時:2014/6/20)投稿日:2014/5/29
.

ロケットの姿勢制御と慣性モーメント
月通常ロケットは上昇のために燃焼室での燃焼による気体の膨張力により、機体を押す。その力の作用点は後部になる。つまり、重心より下になる。このことによって、ヘリコプタのような安定な上昇ができない。
回転角度をθ、トルク(モーメント)をT,完成モーメントをIとすると、
I*d^2θ/dt^2=T ---(1)
という関係がある。
■例
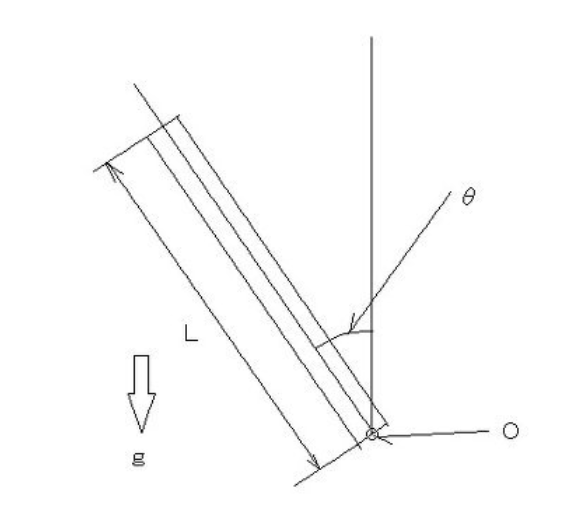
図1 倒立振り子
図1を考える。質量は長さ方向密度とする。つまり、長さ方向の座標をxとすると、質量の長さ密度を考えmとする。これをどこでも一定であるとすれば、慣性モーメンIトと重力によるトルクTgは、
I=∫(0、L)x^2*m*dx=L^3*m/3 ---(2)
Tg=∫(0、L)x*m*g*sin(θ)dx=L^2*m*g*sin(θ)/2--(3)
これが、この倒立振り子の倒れることに関する変数である。そして、この運動を防ぐためのトルクTは、
T=Tg
であるから、トルク作用点での、θ方向の力Fは、
F=Tg/L
ここで、L*m=M、つまり、Lに関係なく全質量Mが同じだとすれば、
I=L^2*M/3 --(4)
Tg=L*M*g*sin(θ)/2 --(5)
F=M*g*sin(θ)/2 --(6)
もし、Tg≠Tであれば、運動する。その運動方程式は、
I*d^2θ/dt^2=⊿T
⊿T=T-Tg
となる。
■スケール変化
もし大きさがn倍になったらどうなるのか?
(4)(5)式より、
I=L^2*M/3
Tg=L*M*g*sin(θ)/2
つまり、
Tg/Iーー>1/L倍
つまり、Mに関係なく、長いほうが、重力による「倒れ速さ」、つまりθの変化はゆっくりになる。
■制御理論
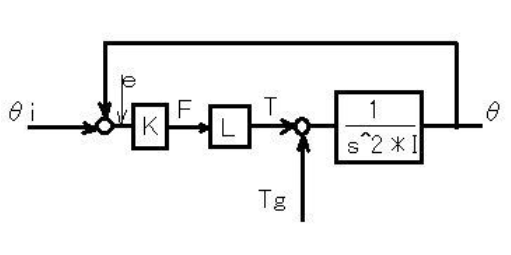
図2 姿勢制御のブロック図
図2において、θiは姿勢の目標値である。この場合ループゲインGは、
G=K*L/(s^2*I)=K*L/(s^2*L^2*M/3)
=3K/(s^2*L*M)
である。Tgに対する応答は、フィードバックがない場合、
θ=Tg/(s^2*I)=(L*M*g*sin(θ)/2)/(s^2*L^2*M/3)
=(3g*sin(θ)/2)/(s^2*L)
となり、Lに反比例して反応は大きく、速くなる。
また、外乱Tgとe(制御器へのIN信号)の関係は、開ループの場合、
e=Tg/(s^2*I)
=(L*M*g*sin(θ)/2)/(s^2*L^2*M/3)
=(3g*sin(θ)/2)/(s^2*L)
つまり、同じ質量Mなら、Lが小さいほど、重力から倒れまでの関係は大きくなる。それだけ制御は困難になる。
http://www.bekkoame.ne.jp/~yoichqge/roc/2000_3_4/Edu/NASA_BOOK/htmls/Practical_Rocketry.htm
http://ci.nii.ac.jp/naid/110008441308