
バンドギャップ電源の発明者ロバート・ワイドラー
LT社と他の2社をあげるが、いずれも、T*In(T)のエラー項を補正するものである。この項に比例した電流をつくり注入している。
■参考
3端子レギュレータ78シリーズの回路解析 - SonofSamlawのブログ (hatenablog.com)
■LT社のLT1019

図1 LT1019回路図
図1ものはLT社の電圧リファレンスであり、温度ドリフトが typ 3ppm/℃ というものである。バンドギャップ型であり、下記の特許回路で2次補正している。
USP 4,603,291
NONLINEARITY CORRECTION CIRCUIT
FOR BANDGAP REFERENCE
1986
が対応している。

図2 USP 4,603,291の図
■準備
USPで冒頭の数式を理解するために、準備として、

より引用する。
******* 引用 **********
Vbe=VtIn(I1/Is)
vbe:ベースーエミッタ間電圧
I1:コレクタ電流
Is=(q*A*ni^2*Dn)/Qb=B*ni^2*Dn=B'*ni^2*T*μn
Qb:ベース中の不純物密度
μn:ベースでの電子の移動度
A:エミッターベースの接合面積
T:温度
B,B’は温度不変、アインシュタインの関係式μ=(q/kT)*DnがIsをμと
ni^2で表すのに用いられている。
μn=C*T^(-n)
と表しておく。
ni^2=D*T^3*exp(-Vg0/Vt)
Vg0:0度Kにおけるシリコンのバンドギャップ推定値
D、C:温度に不変な対して量で内容はこの場合重要でない。
μnの式のnはベース領域の不純物によりきまる。
以上を合わせて、
Vbe=Vt*In(I1)*T^(-γ)*E*exp(Vg0/Vt))
=Vt*In(I1)-γ*Vt*In(T)+Vt*In(E)+Vg0 <---USPでは、これを使っているのか?
γ=4-n
である。
ーーーーー ここで筆者意見 ーーーーーーーーーーー
ここで下の特許のために・・・
未知な値In(E)を消去する方法。
T=T0,I1=I10のときVbe=Vbe0であったとする。すると、
Vbe=Vt*In(I1)-γ*Vt*In(T)+Vt*In(E)+Vg0
Vbe0=Vt0*In(I10)-γ*Vt0*In(T0)+Vt0*In(E)+Vg0
これから、
In(E)=(Vbe0-Vt0*In(I10)+γ*Vt0*In(T0)-Vg0)/Vt0
これをVbeの式に代入して、
Vbe=Vt*In(I1)-γ*Vt*In(T)+Vt/Vt0*(Vbe0-Vt0*In(I10)+γ*Vt0*In(T0)-Vg0)+Vg0
=Vt*In(I1)-γ*Vt*In(T)+(Vbe0*Vt/Vt0-Vt*In(I10)+γ*Vt*In(T0)-Vg0*Vt/Vt0)+Vg0
=Vt*In(I1/I10)-γ*Vt*In(T)+Vbe0*Vt/Vt0+γ*Vt*In(T0)+Vg0*(1-Vt/Vt0)
=Vt*In(I1/I10)+Vbe0*Vt/Vt0+γ*Vt*In(T0/T)+Vg0*(1-Vt/Vt0)
=Vt*In(I1/I10)+Vbe0*Vt/Vt0-γ*Vt*In(T/T0)+Vg0*(1-Vt/Vt0)
ーーー (a)
下の特許ではこれにC1*kT/q(c1*Vt)を加えてVoutとしている。また、下の特許の中のnは上のγと
γ=n
の関係があると思われる。
ここの式が下の特許に使われている。
ーーーーーー 筆者意見終わり ーーーーーーーーーーーー
さらに進めて、

******* 引用終わり ************
■USPより
⊿Vbe=(kT/q))*In(A)
Vout=Vbe+VR4
= Vbe+GVR3
=Vbe+(2R4/R3)*In(A)
また、
Vout=C1*kT/q+Vg0*(1-T/T0)+Vbe0*(T/T0)+(kT/q)*In(Ic/Ic0)
+(nkT/q)*In(T/T0)
(1)
ーーーーーーーーーー 筆者意見 ーーーーーーーーーー
この式は上で導かれた式であるが、最後の項の符号はーの間違いではないかと思われる。Vout=C1*kT/q+Vbeであり、Vbeは上で導かれた形である。
(1)式でIcもTに比例するので4項目からもT*In(T)に比例する成分が出てくる。
上の式で最後の項は(nkT/q)*(In(T)-In(T0))であるから、T*In(T)の補正をすることがこの特許の目的である。
ーーーーーーーー 筆者意見終わり ーーーーーーーーー
これをTで微分すると、
dVout/dT=C1k/q-Vg0/T0+Vbe0/T0+(nkT/q)*(1/T)-(nk/q)*In(T/T0)
+(k/q)*In((ic/Ic0)
ーーーーーーー 筆者意見 ―ーーーーーーーーーーーー
要は、IoとしてT*In(T)に比例した電流を得たいのである。図2において、
Io=⊿Vbe/R41=(Vbe(Q41)-Vbe(Q42))/R41
=(kT/(q*R41))*In((I41/I42)*(A42/A41))
A41,A42:Q41,Q42のエミッタ面積。
ここでI41∝T、I42=一定とすれば、
Io∝T*In(T)
これを図2のQ42のコレクタにいれて(1)式のT*In(T)の項を打ち消そうというわけだ。
点42からIoを抜き取ることによって引き起こされるVref電圧の変化がIoに比例した形で起こるなら(1)式のT*In(T)成分は打ち消されることになる。
(1)式は誤りがあるみたいなので(a)式で考えれば、T*In(T)項はー符号であるとすれば、図2でIoにより、フィードバック回路はVrefを引き上げることによってQ1の電流をより増やし、R1,R2の電圧を等しくする。つまりIoの変化(T*In(T)にそった)に比例してVrefを変化させる。この効果は+符号となりうまく打ち消されることになる。この動作によるQ1のコレクタ電流Icの温度変化は、これがないときのIcの温度変化に比べて無視できるくらい小さくなければならない。
ーーーーーーー 筆者意見終わり ーーーーーーーーーー
■Advanced Micro Dvicesの例
USP 4,443,753
SECOND ORDER TEMPERATURE COMPENSATED BAND GAP
VOLTAGE REFERENCCE
図3 USP 4,443,753の図
42の電流がT*In(T)に比例するようになっている。
■Analog Devicesの例
USP 5,352,973
TEMPERATURE COMPENSATION BANDGAP VOLTAGE REFERENCE
AND METHOD
1994

図4 USP 5,352,973
Rc1の電流がT*In(T)に比例するようになっている。
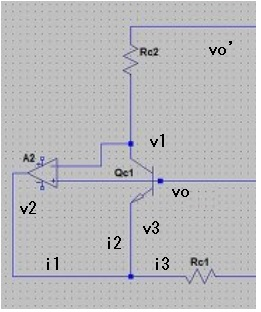
図5

*1:γ―α)*In(T)-In(E*G
